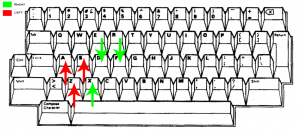
Double Binding
In Armagetron, a player may bind more than one key to a turn direction. For example, binding two keys for a left turn, and then pressing them both simitaniously will result in a quick one-eighty turn-around. Double-binding has a long and glorious history smattered with a fair bit of controversy along the way.
Players can bind as many keys as they want. Some players triple-bind which is great for making "knots" and in very rare cases people bind four keys (quad-bind), though the vast majority of players only double-bind.
Also, players sometimes describe their turns as "doubles" and "triples" even if they only use one key each to make the turns. It can be a little confusing. Sometime people are describing their keyboard actions and sometimes the shape of their turns.
History
The earliest known double binder is Locutus. His reasoning was that since he had a bit of carpal tunnel syndrome, it was easier to play the game if he bound two or more keys to the same actions. So when he started doing it, it was to deal with a condition that might otherwise be considered disabling. You know, kinda like having one of those doughnut pillows to drive.
From there, it started spreading to younger more able-bodied individuals who wanted to exploit it to get the other guy. On the older servers, it wasn't a large problem because if you turned around too quickly against a wall, your cycle bounced.
After a certain period of time, another player by the name of Digital Logic popularized the phrase "Double binding is a crutch of the weak", talked a bunch of trash on the forums, and then ran away when the inevitable challenge came. We had the tournament anyway, it was a lot of fun. Here's the original thread
180s in 0.2.7.1
The double-edged sword that is Armagetron Advanced 0.2.7.1 had a fix for the bounce bug. It also had some refactoring of rubber code. The end result was that it was now possible for all players to turn around quickly against any given wall many times in a row. The double-binding crowd jumped all over it and created a situation many older players considered almost unbearable.